堆排序
1
2
3
4
5堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。
堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
1.大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
2.小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;算法步骤
1
2
3
4创建一个堆 H[0……n-1];
把堆首(最大值)和堆尾互换;
把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
重复步骤 2,直到堆的尺寸为 1。
动图演示

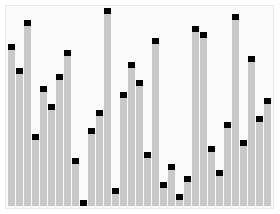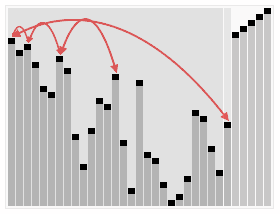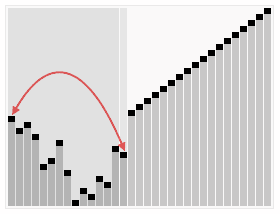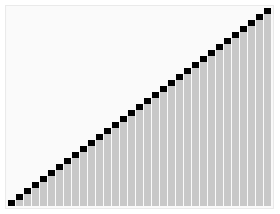
Js实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45function heapSort(arr) {
// 构建最大堆
const n = arr.length;
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 依次取出堆顶元素,放入有序区
for (let i = n - 1; i >= 0; i--) {
// 将堆顶元素(最大值)和当前未排序部分的最后一个元素交换位置
const temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 对剩余元素重新构建最大堆
heapify(arr, i, 0);
}
return arr;
}
function heapify(arr, n, i) {
// 初始化最大值为当前节点
let largest = i;
const left = 2 * i + 1;
const right = 2 * i + 2;
// 如果左节点比最大值大,则更新最大值
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右节点比最大值大,则更新最大值
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大值不是当前节点,则交换当前节点和最大值,并继续向下调整堆
if (largest !== i) {
const temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
heapify(arr, n, largest);
}
}Go实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36func heapSort(arr[]int)[]int {
arrLen:= len(arr)
buildMaxHeap(arr, arrLen)
for i := arrLen - 1; i >= 0; i-- {
swap(arr, 0, i)
arrLen -= 1
heapify(arr, 0, arrLen)
}
return arr
}
func buildMaxHeap(arr[]int, arrLen int) {
for i := arrLen / 2; i >= 0; i-- {
heapify(arr, i, arrLen)
}
}
func heapify(arr[]int, i, arrLen int) {
left:= 2 * i + 1
right:= 2 * i + 2
largest:= i
if left < arrLen && arr[left] > arr[largest] {
largest = left
}
if right < arrLen && arr[right] > arr[largest] {
largest = right
}
if largest != i {
swap(arr, i, largest)
heapify(arr, largest, arrLen)
}
}
func swap(arr[]int, i, j int) {
arr[i], arr[j] = arr[j], arr[i]
}

